理工学部/数学科研究室紹介
代数学分野

ルービックキューブは、置換群に深く
関連しています
- 楕円函数やアーベル函数の研究およびそれらの数論への応用
- 鏡映群上の非可換微分構造と可積分系、および可換代数の組合せ論的研究
- ブラウアー群などの代数多様体の不変量に関する研究とその数論への応用
- 実2次体の基本単数と類数の連分数展開による研究
幾何学分野
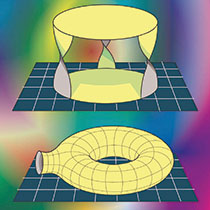
描かれている2つの曲面は、
同じ内在的性質を持っています
- 数理現象の幾何学的視点からの研究
- 幾何学における変分問題に関する研究
- 変換群論と合同類のモジュライに関する研究
- 結び目の位相幾何学的研究
解析学分野
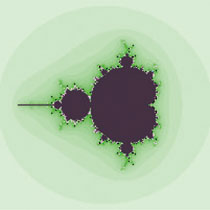
2次多項式の反復合成によって定義された
マンデルブロ集合
- 数学の多くの分野にプロトタイプとして現れる調和関数の研究
- 自然現象から導かれる偏微分方程式の基本解の研究
- 複素変数微分方程式の解の特異点の研究
※図は2次多項式の反復合成によって定義されたマンデルブロ集合です。
簡単なものから作られる複雑性、そして複雑さの中に潜むシンプルな美しさ。
解析学の探究に終わりはありません。
数理情報分野

宇宙の神秘を現しているとされる
『曼荼羅図』は、『シェルピンスキーの
カーペット』と呼ばれるフラクタル図形とも
関係しています
- 無限次元確率解析の理論とその応用
- 確率論、特にエルゴード理論と符号力学系の研究
- 確率論(マルチンゲール理論)と拡散方程式の逆問題
- 確率論・統計学に関するアルゴリズムの研究
計算機科学分野
学生がProcessing(JAVAプログラミング)で
作った「ハノイの塔」です。
- C言語/C++言語プログラミングの整数論・数値解析・数理情報論などへの応用
- 数式処理ソフトを用いた数学およびプログラミングの研究
- JAVAプログラミング/JavaScriptプログラミング
- 組み込みプログラミング








